As promised, here are the performance results for my OpenMP implementation of mergesort.

threads	- -tasking (sec)-	-sections (sec)-
2	78.9607	79.6218
4	46.2879	45.4269
8	28.8564	28.1636
16	22.3226	22.0314
32	21.5526	21.5884
64	21.7181	21.1851

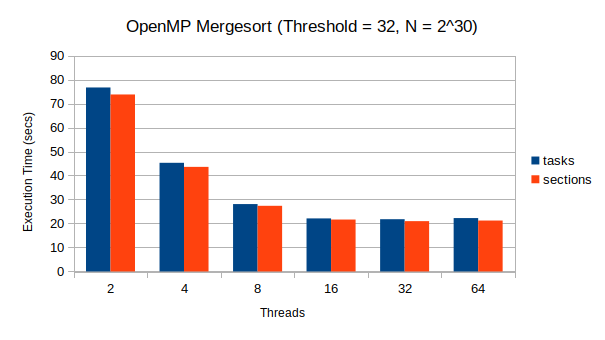
These are the average of 10 runs with each of the different thread counts. These experiments were run on an AMD Ryzen 7 - 1700 8-Core machine with 16 hardware threads and an array of 2³⁰ random integers.

You can see that there is a good performance improvement when the number of threads is increased, which bottoms out once the number of system hardware threads has been reached (16 in the case of this experiment). As you’ve probably noticed, the performance is very similar between tasks and sections implementations, with sections being slightly more performant. This is likely because there is a slight overhead due to the dynamic queuing nature of tasking, as tasks are placed in a queue before being assigned to threads. This dynamic behaviour is one of the major benefits of using tasks.

The reason I was able to get similar performance from sections is because I kept track of the recursion depth in the sections implementation so that 16 threads would be used, reverting to serial mergesort once this depth had been reached. This depth checking is not needed in the tasking version, as the task queue allows for automated thread management when using nested parallelism, and thus makes for slightly simpler code. However, even with this thread count/depth checking, tasking would often see some performance increases over using sections, as the load can be better balanced. Once a thread completes a task it is returned to the pool, and a new task is assigned to it. Tasking also allows for the preemption of threads in some cases. Sections, on the other hand, have an implicit barrier at the end of a #sections pragma which wait for all sections to complete before moving on.

The reason no performance is gained in this case is likely because mergesort is a naturally balanced algorithm; the partitions are always the same size (or very close to the same size). Tasking will likely outperform sections on an algorithm like Quicksort, where the varying pivot point leads to different sized partitions and therefore, load imbalance between tasks. So with that said, this week I will implement 2 versions of Quicksort; one using OpenMP sections, and the other utilizing the tasking contruct.

Check in next week for a discussion of my 2 implementations of parallel Quicksort!